Cosine Rule on a Sphere

As all (well, at least those that can remember) 15+ year olds know, to find the length of a side of a non-right angled triangle you can’t use Pythagoras’ theorem and instead require the so called ‘Cosine Rule’.

Simply, the cosine rule is used to find (for example) the length of side \(c\) in:

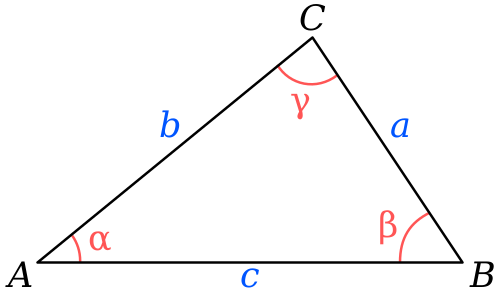
You use the following formula:

\[c^2 = a^2 + b^2 - 2ab\cos(\gamma).\]

But what happens if we move away from Euclidean Geometry and that our triangle is now sitting on a sphere? I.e.

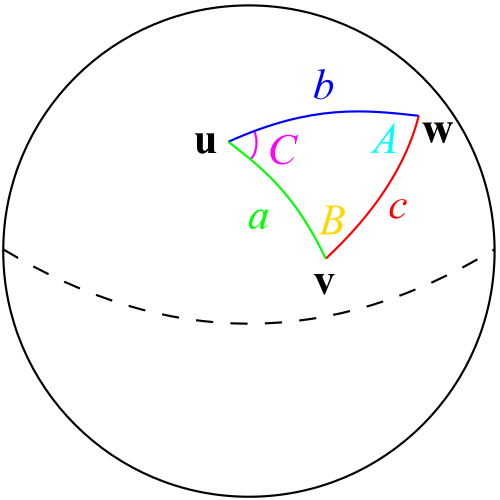
Logic tells us that of course the same cosine rule can not be applied to find the side \(c\). Instead we use an alternative formula, namely:

\[\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C).\]

The proof is relatively straight forward, try having a go before looking below:

Let \(\textbf{u}\), \(\textbf{v}\) and \(\textbf{w}\) be unit vectors from the middle of the sphere to the points \(u\), \(v\) and \(w\) of our triangle. The lengths of the sides are then give by the dot product:

\[\begin{eqnarray*} \cos(a) &=& \textbf{u}\cdot\textbf{v},\\ \cos(b) &=& \textbf{u}\cdot\textbf{w},\\ \cos(c) &=& \textbf{v}\cdot\textbf{w}. \end{eqnarray*}\]

The angle \(C\) is the inverse cosine of two tangents, say \(\textbf{t}_a\) and \(\textbf{t}_b\), which are along the sides \(a\) and \(b\), i.e.

\[\begin{eqnarray*} C &=& \cos^{-1}(\textbf{t}_a\cdot\textbf{t}_b),\\ \cos(C) &=& \textbf{t}_a\cdot\textbf{t}_b. \end{eqnarray*}\]

But we know more information about these tangent vectors. For instance we know that the they are perpendicular to \(\textbf{u}\) which is given by the component of \(\textbf{v}\) perpendiculat to \(\textbf{u}\).

This gives (once normalized):

\[\textbf{t}_a=\frac{\textbf{v}-\textbf{u}(\textbf{u}\cdot\textbf{v})}{|\textbf{v}-\textbf{u}(\textbf{u}\cdot\textbf{v})|} = \frac{\textbf{v}-\textbf{u}\cos(a)}{\sin(a)}.\]

Similarly,

\[\textbf{t}_b=\frac{\textbf{w}-\textbf{u}(\textbf{u}\cdot\textbf{w})}{|\textbf{w}-\textbf{u}(\textbf{u}\cdot\textbf{w})|} = \frac{\textbf{w}-\textbf{u}\cos(b)}{\sin(b)}.\]

So substituting these values into the above equation we get:

\[\begin{eqnarray*} \cos(C) &=& \frac{\textbf{v}-\textbf{u}\cos(a)}{\sin(a)}\cdot \frac{\textbf{w}-\textbf{u}\cos(b)}{\sin(b)},\\ \cos(C) &=& \frac{\textbf{v}\cdot\textbf{w}-(\textbf{v}\cdot\textbf{u})\cos(b)-(\textbf{u}\cdot\textbf{w})\cos(a)+(\textbf{u}\cdot\textbf{u})\cos(a)\cos(b)}{\sin(a)\sin(b)},\\ \cos(C) &=& \frac{\cos(c)-\cos(a)\cos(b)}{\sin(a)\sin(b)}. \end{eqnarray*}\]

Which when rearranged gives the required cosine rule:

\[\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C).\]

Follow this link if you want to see the sine rule on a sphere.