Sine Rule on a Sphere

A couple of days ago I wrote about how to find the cosine rule on a sphere. In this post I’ll show you the sine rule on a sphere.

Consider the following triangle on a sphere:

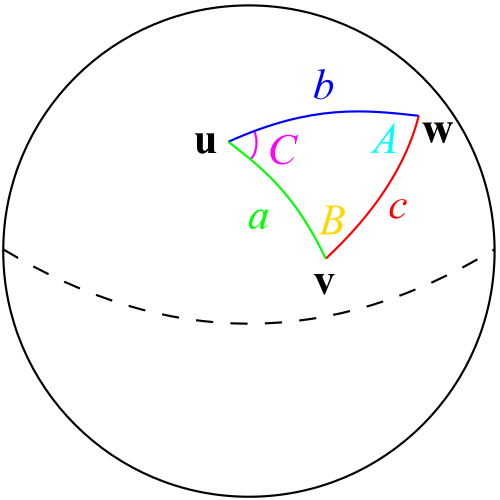
The cosine rule (on a sphere) is:

\[\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C).\]

The sine rule is then, where \(A\) is the angle at \(\textbf{w}\) (opposite side \(a\)) and \(B\) is the angle at \(\textbf{v}\) (opposite side \(b\)):

\[\frac{\sin(A)}{\sin(a)}=\frac{\sin(B)}{\sin(b)}=\frac{\sin(C)}{\sin(c)}.\]

The proof is a simply a rearranging exercise from the cosine rule, with the formula \(\cos^2(C)+\sin^2(C)=1\). You can find the proof below, but I do recommend having a go yourself.

Rearrange \(\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C),\) to get:

\[\cos(C)=\frac{\cos(c)-\cos(a)\cos(b)}{\sin(a)\sin(b)}.\]

Now we use \(\sin^2(C)=1-\cos^2(C)\) substituting the above in for \(\cos^2(C)\):

\[\begin{eqnarray*} \sin^2(C) &=& 1-\left(\frac{\cos(c)-\cos(a)\cos(b)}{\sin(a)\sin(b)}\right)^2,\\ \sin^2(C) &=& \frac{\sin^2(a)\sin^2(b)-(\cos(c)-\cos(a)\cos(b))^2}{\sin^2(a)\sin^2(b)}. \end{eqnarray*}\]

Now again use \(\sin^2(C)=1-\cos^2(C)\) but for \(a\) and \(b\) to get:

\[\sin^2(C)=\frac{(1-\cos^2(a))(1-\cos^2(b))-(\cos(c)-\cos(a)\cos(b))^2}{\sin^2(a)\sin^2(b)}.\]

Times everything out and cancel to get:

\[\sin^2(C)=\frac{1-\cos^2(a)-\cos^2(b)-\cos^2(c)+2\cos(a)\cos(b)\cos(c)}{\sin^2(a)\sin^2(b)}.\]

Finally divide everything by \(\sin^2(c)\) to get the required form:

\[\frac{\sin^2(C)}{\sin^2(c)}=\frac{1-\cos^2(a)-\cos^2(b)-\cos^2(c)+2\cos(a)\cos(b)\cos(c)}{\sin^2(a)\sin^2(b)\sin^2(c)}.\]

Which is what we wanted, since the right hand side is symmetrical in \(a\), \(b\) and \(c\), i.e.

\[\frac{\sin^2(A)}{\sin^2(a)} = \frac{\sin^2(B)}{\sin^2(b)} = \frac{\sin^2(C)}{\sin^2(c)}.\]

But since our angle must be between \(0\) and \(\pi\), all the terms are positive, so we can take the square root to get the sine rule on a sphere:

\[\frac{\sin(A)}{\sin(a)}=\frac{\sin(B)}{\sin(b)}=\frac{\sin(C)}{\sin(c)}.\]