Velocity Required for Loop-the-Loop

In this post we are going to work out (approximately) the minimum speed required to complete a loop-the-loop, we’ll do this via an energy argument. However, for ease, we are going to ignore friction! First we need to find the minimum speed required at the top of the loop.

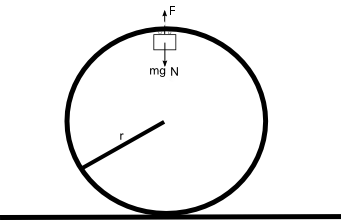
To get the minimum required speed to make the loop-the-loop, at the top of the loop we require the normal force (\(N\)) to be \(0\). Equating the forces at the top of the loop we have the weight of the car (\(mg\)) plus the normal force (\(N\)) equal to the centrifugal force (\(F\)), which is given by \(F=\frac{mv^2}{r}\) where \(r\) is the radius of the circle. Thus,

\[\begin{eqnarray*} \frac{mv_t^2}{r} &=& N+mg, \\ \frac{v_t^2}{r} &=& g,\\ v_t^2 &=& gr,\\ v_t &=& \sqrt{gr}. \end{eqnarray*}\]

Giving us a minimum velocity at the top of the loop, \(v_t\). We now proceed with the energy argument.

The total energy at the top of the loop is equal to the potential energy at the top plus the kinetic energy at the top, respectively these are:

\[\begin{eqnarray*} PE_t &=& mgh = 2mgr,\\ KE_t &=& \frac{1}{2}mv_t^2 = \frac{1}{2}mgr. \end{eqnarray*}\]

Thus the total energy at the top is:

\[\begin{eqnarray*} E_t &=& 2mgr+\frac{1}{2}mgr,\\ &=& \frac{5}{2}mgr. \end{eqnarray*}\]

We now find the total energy at the bottom, since there is no potential energy, this is simply the kinetic energy,

\[E_b = \frac{1}{2}mv_b^2.\]

Where \(v_b\) is the speed we are looking for. With our assumptions, the energy at the top (\(E_t\)) equals the energy at the bottom (\(E_b\)) giving

\[\begin{eqnarray*} E_b &=& E_t,\\ \frac{1}{2}mv_b^2 &=& \frac{5}{2}mgr,\\ mv_b^2 &=& 5mgr,\\ v_b^2 &=& 5gr,\\ v_b &=& \sqrt{5gr}. \end{eqnarray*}\]

Thus we have found the speed required to complete a loop the loop of radius \(r\). For example, if the loop had a 4 metre diameter (2 metre radius) then the velocity required to complete the loop would be \(v = \sqrt{5\times g\times 2}=\sqrt{10g}\approx 9.9\).

For convience we can approximate \(\sqrt{5gr}\) as:

\[\sqrt{5\times 9.81\times r}=\sqrt{49.05r}\approx 7\sqrt{r}.\]