- mathematics
- football
- code
- spaceWeather
- misc
- MathsOnAMug
•
•
•
•
•
-
Football Bogey Grounds and How Statistics Can Prove Them
Can a football club actually have a statistically verifiable football bogey ground or is it just bad luck?

-
40 points to avoid relegation?
40 points is the classic benchmark to avoid relegation from the Premier League, is this the right value?

-
New space weather modelling suite enables upper atmosphere forecasting
New suite of space weather forecasting models focuses on how space weather can influence the thermosphere and ionosphere here on Earth.

-
The Trend in Taylor Swift's Mood
Taylor Swift doesn't just release albums, she releases chapters of her life, but can we see that story in the music itself?

-
Pour Over Brewing Recipe Generator
Generate pour over brewing coffee reciepes for a given bean

-
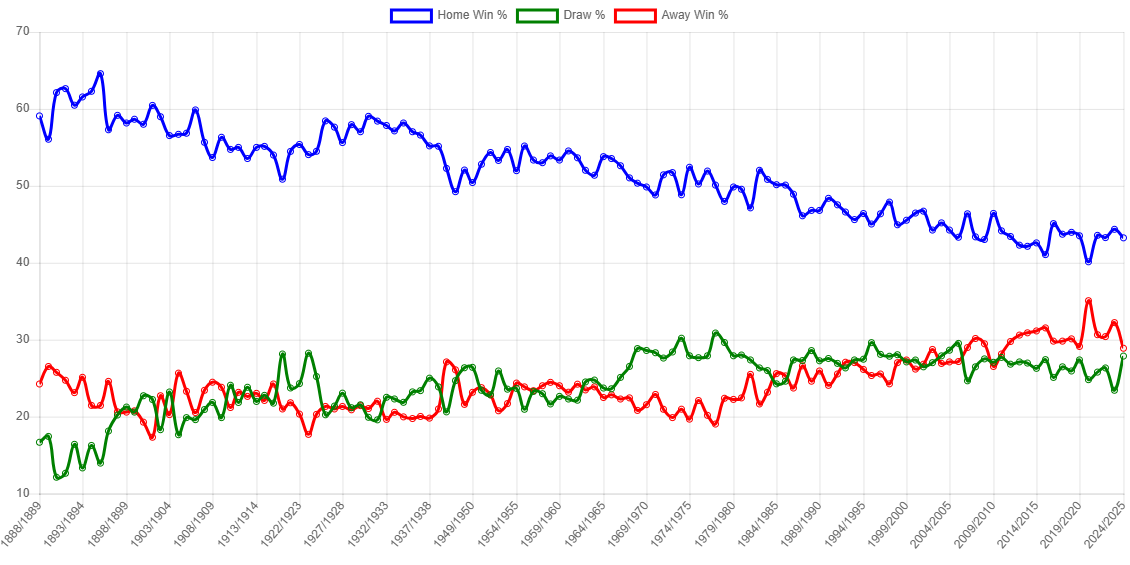
Waning Home Advantage in English League Football
An investigation in the trend of home advantage in English football
-
Brewing the Perfect Coffee at Altitude
Why your coffee tastes different in Boulder, CO compared to Birmingham, UK.

-
All England football league results
A plain text set of all England football (soccer) league results from 1888 to present.

-
How aerodynamic is Santa
Santa is at the top of many engineering disciplines - his production line for presents, for example. However one that is often overlooked is the space-domain (Redirect to University of Birmingham News page)

-
Levelling the Playing Field, Adjusting Goal Records in International Football
By weighting international goals by strength of the opposition we can compare goal scoring prowess across the decades.
