Could Jack Dawson (Leonardo DiCaprio) and Rose DeWitt Bukater (Kate Winslet) from the motion picture ‘Titanic’ both have survived by both floating on the door? (Clearly there are a load of spoilers in this article – but the film did come out over 20 years ago so I’m not going to worry too much about it).
[Note: This is a copy of an article I wrote in 2011, which is no longer available online so I’ve repeated it here for prosperity]
Introduction
During the 1997 motion picture ‘Titanic’ by James Cameron there is a famous scene involving the two main characters, Jack Dawson (as played by Leonardo DiCaprio) and Rose DeWitt Bukater (Kate Winslet) towards the end of the film. The scene involves Jack in the ocean and Rose floating on a wooden object, Jack dies and Rose survives, however the question we ask is, need Jack of died? Was there room (and spare buoyancy) for two? This is a question which appears repeatedly (e.g. [1] and [2]) on the internet but with varying answers, but hopefully this article can draw a conclusion to the discussion.
The first point to settle is that Rose is not floating on a door and is instead floating on a piece of wood panelling. The panelling in the film is based upon a recovered piece, homed at the Maritime Museum of the Atlantic, in Halifax, Nova Scotia [3].
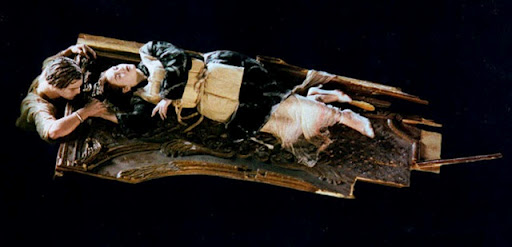
There are two main issues that need to be resolved:
- Could they both have fit on the panelling?
- Would their combined weight have been greater than the upward force due to buoyancy (i.e. would they have sank)?
Eureka!
In this section we introduce the basics of buoyancy, which will be crucial in the later sections.
The history of buoyancy is a long one, and has provided one of the most famous stories in science. Archimedes supposedly exclaimed “Eureka!” when he discovered a fundamental principle of buoyancy, which relates buoyancy to displacement. Indeed this principle is still named after him, and first appears as Proposition 5 in [4].
Archimedes Principle:
Any solid lighter than a fluid will, if placed in the fluid, be so far immersed that the weight of the solid will be equal to the weight of the fluid displaced.
This tells us that the buoyancy force, \(F_B\), is equal to the weight, \(W\), of the object placed in the fluid, so \(F_B = W.\) Weight is equal to the mass of the object times gravity, \(g\), and mass is equal to density, \(\rho\), times volume, \(V\), giving rise to the more well known equation:
\begin{equation}
F_B=\rho Vg.
\end{equation}
Could they both fit?
The first question to resolve is, “Could Rose and Jack have both fit on the panelling?”.
The solution to this problem has been ‘demonstrated’ previously:
However, both of them fitting on the panel is not where the problem lies.
Variables
Before we can dive into the problem of buoyancy we first need to consider a number of variables which will need to be approximated. Namely:
- What is the size of the panel?
- What is the density of the panel (what is it made from)
- What is the mass of Rose?
- What is the mass of Jack?
- What is the density of the water
Panel Size
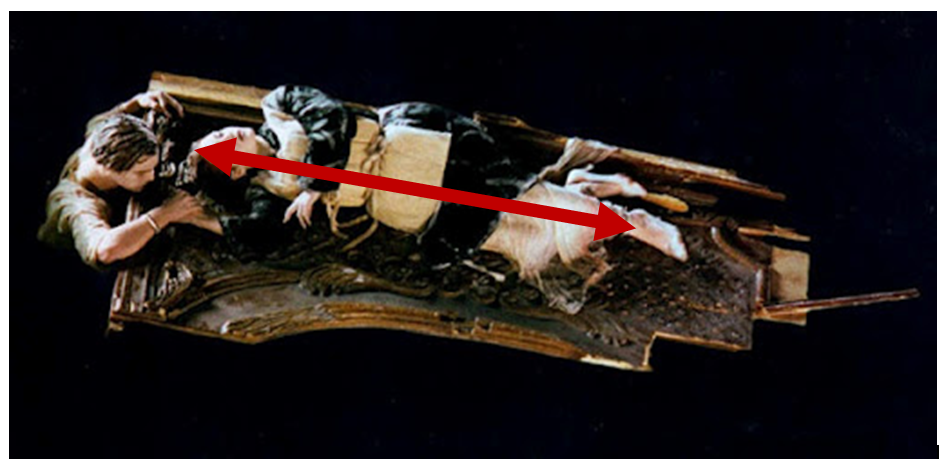
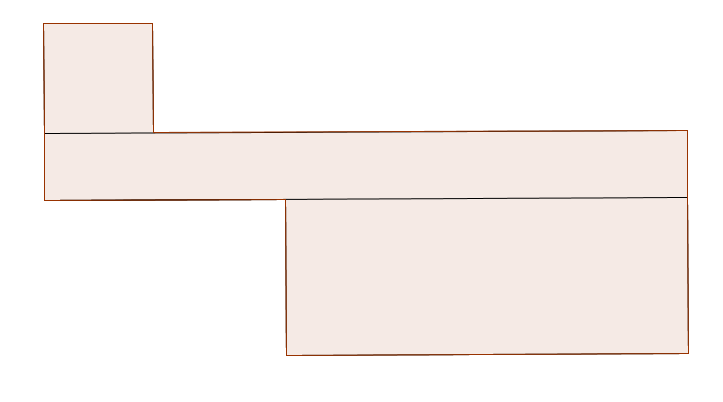
First off we approximate the size of the panelling. A common mistake (or at least a common oversight) when approaching this problem is taking the panelling to be a rectangle. This is obvious from the overhead shot of the panelling and so I’ve created a more reasonable approximation of the panelling:
Now that we have the shape of the panelling we need to find the correct dimensions. All that is required is the length of one of the sides, and everything else can be calculated from that scale. From personal communication with the Maritime Museum of the Atlantic the size of the actual panel which the fictional one is based on is 150 cm by 105 cm by (~)3 cm (“the thickness of this panel is not recorded in the record, it is currently behind glass and is estimated at 3 cm”). However we can quickly see that the panelling in the film is larger than this, we can see this by comparing it with Rose’s height.
It is a pretty safe assumption that Rose’s height is equal to Kate Winslet’s height, and she is quoted as saying she is 5 foot 6 inches (167.6 cm) [6]. This now gives the scale factor for the panelling (comparing the height of Rose to the length of the panel):
Using this scaling factor gives the visible area of the panelling to be \(1.91 \mbox{m}^2\).
This leaves the question of the depth of the panelling, something which is considerably harder to find. There are very few images that provide a clue of the depth, and they are not conclusive:
There are a multitude of issues with getting the scale from these images, mainly due to the angle of the camera. The first image seems to imply a depth of approximately 0.1 metres, which we find, via scaling, from Jack’s hand. However we can see that the edge which is above the water is clearly thicker than the rest of the door. Something that should be considered (especially when calculating the mass of the door). In the other figures we see that the panelling gets considerably thicker (about twice as thick again) further down (the section is underwater in the first figure). We are left to speculate whether this extra depth covers the whole of the panel, as in:
or just a small section as in:
or anything in between. In both of these cases the head on view of the panelling is the same:
There can be no way of knowing for sure which possibility is the correct one. However the first option would result in a considerable mass, which would probably result in the panelling not being able to float, which we know is a fallacy. So for the rest of the document we consider that we are in the second case.
Rose’s Mass
Again, let us assume that Rose’s mass is the same as Kate Winslet’s. This is hard to pin down, but via various internet sources this appears to be between \(54\) and \(59 \mbox{kg}\) [7,8], so, for an approximation, we take the midpoint and use \(56.5 \mbox{kg}\). It is also worth noting that the wet clothes that Rose was wearing would have added a considerable mass to this total. However, for simplicity, we ignore this factor.
Jack’s Mass
For Jack’s mass we use Leonardo DiCaprio’s mass, which is between \(72.5\) and \(75 \mbox{kg}\) [9]. So, for our calculations, we use \(74 \mbox{kg}\). Again this would have been greater due to the wet clothes.
Panel Density
The density of the wood panelling is key in our study as this will determine the mass of the panel, which is an important factor on whether the panelling will sink or float. We can immediately deduce some bounds on the density, thanks again to the Maritime Museum of the Atlantic in Halifax. According to the museum the piece of panelling is made of oak. Then from [10] the density of oak varies between \(600\) and \(900\mbox{kg m}^{-3}\). Initially a value of \(750\mbox{kg m}^{-3}\) (the midpoint) is used and then later look at what values of panel density would require which panel depths.
Panel Mass
Using the panel density the mass of the panel can be calculated.
The volume of the panel in Figure 9 can be found by calculating the volume of the three individual sections which make up the panel. The ‘top’ section has a volume of \(0.013\mbox{m}^3\). The ‘middle’ section \(0.19\mbox{m}^3\) and finally the ‘bottom’ section is \(0.011\mbox{m}^3\). This gives a total volume of \(0.214\mbox{m}^3\). Which, using the density value from the previous section, equates to a mass of \(160.5\mbox{kg}\).
Water Density
The density of water depends on two main factors, its temperature and the water salinity.
On the night of the Titanic’s sinking the water temperature was reported to be 31 degrees Fahrenheit [11,12], which is approximately \(-0.56^{o}\mbox{C}\).
The salinity of ocean water varies with location. The Atlantic Ocean, where the Titanic sank, varies between 33 and 37 parts per thousand. According to NASA [13] the approximate salinity value of the Atlantic at the location where the Titanic sank (\(41^{o}43.5’\mbox{N } 49^{o}56.8’\mbox{W}\)) is 36 parts per thousand. We can then use the water density calculator provided at [14] with the above values to find a calculated water density of \(1029\mbox{kg m}^{-3}\).
Buoyancy
We now come to the crux of the problem. Could the panelling have supported both Jack and Rose?
First we consider the case which occurred in the film, Rose lying on the panelling. To do this we consider the forces acting upon the panelling, the downward force due to weight, and the upward force due to buoyancy. The only variable we do not know is the displaced volume. Since we know the area of the panel which is in contact with the water we are left to find the height that makes up the submerged portion of the panelling. Thus we actually find the depth to which the panelling sinks, clearly we require this to be greater than the total depth of the panel, in order for some of it to remain above water. We equate the buoyancy force, \(F_B\), with the total weight in the system. We use \(M_R\), \(M_P\) and \(M_J\) to represent the mass of Rose, the panel and Jack respectively.
\begin{eqnarray}
F_B &=& W,\\
\rho Vg &=& (M_R+M_P)g,\\
\rho V &=& M_R+M_P,\\
1029 \times 1.9 \times H &=& 56.5+160.5, \\
1955H &=& 217,\\
H &=& 0.111.
\end{eqnarray}
Which says that the door sinks \(11.1\mbox{cm}\), but we only assumed a panel depth of \(10\mbox{cm}\)! Thus, using our assumptions, Rose could not have floated on top of the panel and been completely above the water. However, since the only real knowledge of this system is that Rose can float on the panel we must adjust our assumptions.
The first assumption to try changing would be our choice of wood density, since this was chosen to be the midpoint of a fairly large range. By rearranging Equation 5 we can plot a graph of densities against how much the panelling would sink:
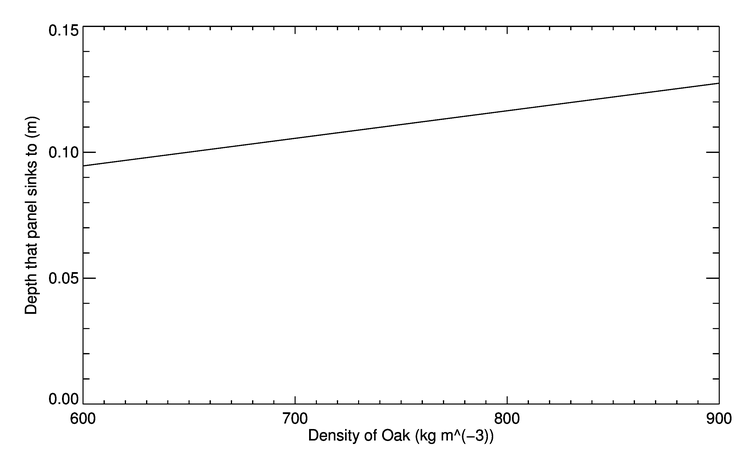
This shows that the least the panel would sink is approximately \(0.095\) metres, which is less than the current assumed depth of the panel. Thus, if we assume a wood density of \(600\mbox{kg m}^{-3}\) then Rose could, like in the film, float on the panelling.
This value of wood density gives a panel mass of \(128.4\mbox{kg}\). Using this panel mass we can calculate that the panelling would sink \(0.066\) metres if nothing was on it, i.e. there would be approximately \(3.5\) centimetres floating above the water. This is a reasonable value, especially when you consider the Figure below:
If we now repeat the above process, using the new panel mass, but also include Jack’s mass we can see whether Jack could also have floated on the panel.
\begin{eqnarray}
\rho Vg &=& (M_R+M_P+M_J)g,\\
\rho V &=& M_R+M_P+M_J,\\
1029 \times 1.9 \times H &=& 56.5+128.4+74, \\
1955H &=& 258.9,\\
H &=& 0.132.
\end{eqnarray}
So the panel would have sank \(0.132\) metres, or just over \(13\) centimetres, some \(3\) centimetres greater than the depth of the panelling.
Conclusion
In summary, both Jack and Rose could have fitted on the piece of wooden panelling, but had they both have got on, the panel would have been submerged under water by \(3.2\) centimetres. However, it is likely that should they both have been on the panelling, they both would have survived (especially if they had sat). This is since the cooling rate is directly related to the amount of exposed surface area and body parts immersed in the water and the best chance of surviving accidental immersion in cold water (\(<20^{o}\mbox{C}\)) is to keep as much of the body as possible out of the water at all times [12].
Jack certainly would have had a much better chance of survival, compared to the almost zero percent chance he had by staying in the water:
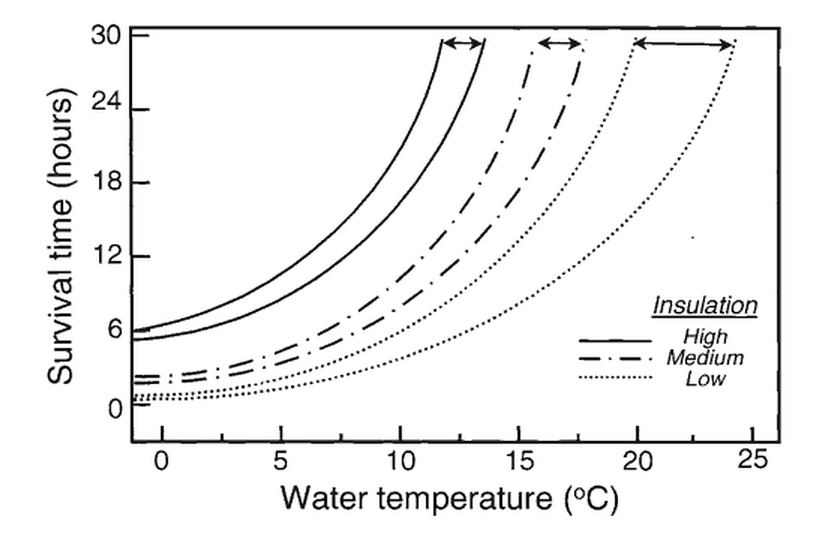Figure 13. Human survival time in cold water.
The curves in the Figure indicate the expected survival times at different levels of body insulation in cold water. Low insulation is light or no clothing, medium is wet suit, and high is dry suit. Dashed lines indicated ranges at low or high body mass [12]. This shows that the length of time Jack could have survived in the water would have been approximately 30 minutes. Indeed, only one person who entered the water after the sinking of the Titanic, and was in it for more than a few minutes, survived the ordeal [12].
So there was room on the door (panelling) for two.
References
[1] https://funypicforyou.blogspot.co.uk/2012/05/titanic-floating-door-facts-explained.html
[2] https://www.reddit.com/r/funny/comments/sf1v2/ill_never_let_go_the_titanic_door_experiment/
[3] http://www.imdb.com/title/tt0120338/trivia?tab=tr&item=tr1076740
[4] Archimedes of Syracuse (1897) The Works of Archimedes, edited in modern notation, with introductory chapters by T.L. Heath
[5] https://www.huffingtonpost.co.uk/2012/04/18/%20jack-and-rose-titanic-plank-of-wood_n_1434092.html
[6] http://news.bbc.co.uk/1/hi/entertainment/2751869.stm
[7] https://www.celebheights.com/s/Kate-Winslet-109.html
[8] http://www.bangla2000.com/entertainment/celebrities/kate_winslet.shtm
[9] https://www.answers.com/Q/What_is_Leonardo_DiCaprio%E2%80%99s_height_and_weight
[10] https://www.engineeringtoolbox.com/wood-density-d_40.html
[11] Haisman D. (2009) Titanic: The Edith Brown Story. AuthorHouse, Bloomington, Indiana.
[12] Piantadosi, Claude A. (2003) The Biology of Human Survival: Life and Death in Extreme Environments. Oxford University Press, Oxford, United Kingdom.
[13] https://science.nasa.gov/earth-science/oceanography/physical-ocean/salinity/
[14] http://www.csgnetwork.com/h2odenscalc.html